Trong toán học, có lẽ chúng ta đã quá quen thuộc với hình tròn nhưng lại có rất nhiều người còn nhầm lẫn giữa hình tròn và đường tròn? Vậy đường tròn là gì? Công thức tính chu vi đường tròn 165 như thế nào? Hãy cùng chúng lời trả lời từng câu hỏi này trong bài viết dưới đây.
Đường tròn là gì?
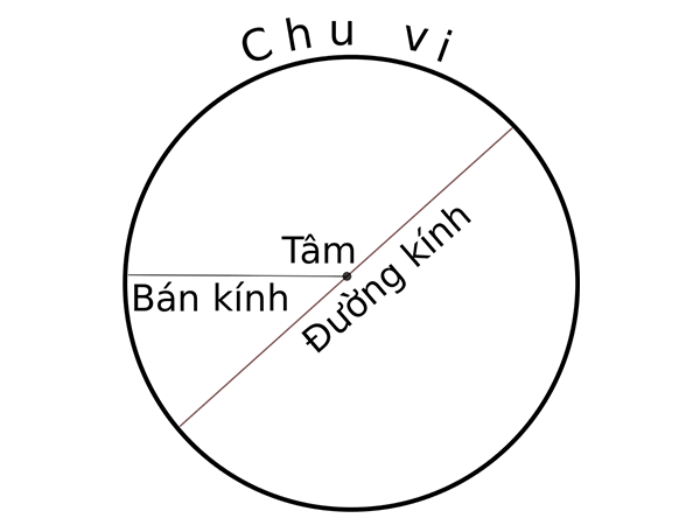
Đường tròn hay còn gọi là vòng tròn là tập hợp của tất cả những điểm trên cùng một mặt phẳng, cách đều một điểm cho trước với một khoảng cách nhất định. Trong đó, điểm cho trước gọi là tâm của đường tròn, còn khoảng cho trước gọi là bán kính của đường tròn.
Khác với đường tròn, hình tròn là tập hợp tất cả các điểm nằm cả bên trong và bên trên đường tròn. Hình tròn bao gồm cả đường tròn và tập hợp các điểm nằm bên trong đường tròn. Tập hợp các điểm cách tâm của đường tròn một khoảng nhỏ hơn hoặc bằng bán kính chính là hình tròn.
Trong đường tròn, đoạn thẳng đi qua tâm của đường tròn, cắt đường tròn tại hai điểm gọi là đường kính. Đường kính là dây cung lớn nhất trong đường tròn và có độ dài gấp đôi bán kính.
Cách tính diện tích hình tròn và chu vi hình tròn
Chu vi hình tròn
Chu vi hình tròn hay độ dài đường tròn là một đại lượng toán học có tính ứng dụng thực tế cao. Ví dụ, nhờ chu vi hình tròn chúng ta có thể đo được quãng đường di chuyển của xe dựa vào số vòng lăn của bánh xe… Vì thế các em học sinh cần phải ghi nhớ kỹ công thức tính chu vi hình tròn là:
- C = d.3,14 (trong đó, C là ký hiệu của chu vi hình tròn và d là ký hiệu đường kính)
- C = 2.r.3,14 (trong đó, C là ký hiệu chu vi hình tròn, r là ký hiệu của bán kính)
Diện tích hình tròn
Diện tích hình tròn là diện tích phần nằm bên trong của hình tròn. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với chính nó và số pi = 3,14. Cụ thể:
- S = r.r.3,14 ( trong đó S là diện tích hình tròn, r là bán kính)
Các dạng bài tập liên quan đến chu vi và diện tích hình tròn
Dạng 1: Tính chu vi và diện tích hình tròn cơ bản
Các dạng bài tập về chu vi hình tròn rất đa dạng từ dễ đến khó. Dạng cơ bản thường sẽ cho trước bán kính hoặc các gợi ý để tìm ra bán kính của hình tròn, từ đó yêu cầu tính chu vi và diện tích hình tròn. Dựa vào công thức, các em có thể dễ dàng tính toán được hai đại lượng này.
Ví dụ minh họa:
Ví dụ 1: Cho một đường tròn tâm A, biết bán kính của đường tròn là 20cm. Tính chu vi của đường tròn.
- Lời giải: Chu vi của đường tròn tâm A là: C = 2r.3,14 = 2.20.3,14 = 125,6 cm
Ví dụ 2: Một bánh xe lăn từ vị trí A đến vị trí B hết 12 vòng. Tính quãng đường AB biết đường kính của bánh xe là 30cm.
- Chu vi của bánh xe là: C = D.3,14 = 30.3,14 = 94,2 cm
- Vậy đoạn đường AB có khoảng cách là: AB = 12.94,2 = 1130,4 cm
Ví dụ 3: Sân trường D hình chữ nhật với kích thước là: chiều dài 45m và chiều là 6,5m. Chính giữa sân của trường có thiết kế 1 bồn hoa hình tròn với đường kính 3,2m. Tính diện tích sân trường?
- Ta có, diện tích sân trường và bồn hoa là: 45.6,5 = 292,5m2
- Diện tích bồn hoa là: (3,2/2).(3,2/2).3,14 = 8,04m2
- Vậy diện tích của sân trường là: 292,5 – 8,04 = 284,46 m2
Một số bài tập tham khảo:
- Bài 1: Trong tòa nhà văn phòng H, người ta đặt 2 bồn trồng hoa hình tròn. Một bồn trồng hoa cúc với bán kính 20 dm. Bồn còn lại trồng hoa hồng có chu vi 9,42 m. Hỏi bồn hoa nào có diện tích lớn hơn và lớn hơn bao nhiêu?
- Bài 2: Một hồ nước hình tròn có đường kính 20m. Giữa bồn nước người ta xây dựng một tháp hình tròn có bán kính 2m. Tính diện tích mặt nước của hồ nước biết mặt nước trùng với thành hồ.
Dạng 2: Biết chu vi/diện tích hình tròn. Tính bán kính/đường kính?

Ở dạng toán này, đề bài thường cho trước, chu vi hoặc diện tích của hình tròn. Từ đó yêu cầu học sinh tính toán ra bán kính, đường kính của hình tròn đó. Phương pháp giải bài toán này vẫn áp dụng những công thức tính chu vi đường tròn, diện tích đường tròn để tìm ra đường kính, bán kính. Một số bài nâng cao sẽ cho tổ hợp của nhiều hình tròn lớn, nhỏ khác nhau trong cùng một mặt phẳng nên các em học sinh cần lưu ý tránh nhầm lẫn giữa các đường tròn với nhau.
Ví dụ minh họa 1: Một hình tròn tâm O có chu vi là 6,28cm. Tính diện tích hình tròn đó.
Lời giải
Ta có:
- d . 3,14 = C
- d . 3,14 = 6,28
- d= 6,28/3,14
- d = 2
Vậy đường kính của hình tròn tâm o là 2cm
Bán kính của đường tròn là:
2/2 = 1(cm)
Diện tích của hình tròn là:
1.1.3,14 = 3,14 (cm2)
Xem thêm: Tính chiều dài chiều rộng hình chữ nhật
Ví dụ minh họa 2
Cho hình vẽ
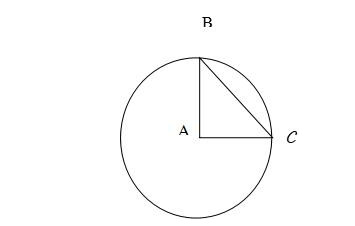
Tam giá ABC là tam giác vuông tại A. Hỏi diện tích hình tam giác vuông ABC trong hình vẽ là bao nhiêu, biết hình tròn tâm A có chu vi là 37,68 cm.
Lời giải
Hình tròn tâm A có
- C= 37,68 cm
Hình tròn tâm A có bán kính là:
- R = C/(2.3,14) = 37,68/(2.3,14) = 6 cm
- Dựa vào hình trên ta có, R = AB = AC
- Diện tích hình tam giác vuông ABC trong hình trên là:
- S = AB.AC/2 = 6.6/2 = 18 cm2
Một số bài tập tham khảo:
- Bài 1: Một cái nong hình tròn có chu vi đo được 376,8cm. Hỏi diện tích của cái nong là bao nhiêu mét vuông?
- Bài 2: Sân trường đại học H có dạng hình thang. Trong đó trung bình cộng hai đáy 40m, chiều cao 30m. Giữa sân, người ta xây một bồn trồng hoa hình tròn có chu vi là 12,56m. Tìm diện tích sử dụng của sân trường đại học H?
- Bài 3: Một chiếc cối xay gạo có hình tròn với chu vi là 119,32 cm. Tìm bán kính và đường kính của chiếc cối xay đó.
Chu vi đường tròn là một chủ đề toán học không quá phức tạp nhưng đặc biệt quan trọng vì kiến thức này sẽ còn áp dụng rất nhiều cho quá trình học tại cấp 2 và cấp 3 cũng như cả đời sống hàng ngày. Hi vọng rằng bài viết trên đây của chúng tôi sẽ giúp các em học sinh dễ dàng hiểu đường tròn là gì? Công thức tính chu vi đường tròn 165 hiệu quả và làm quen với các dạng toán liên quan đến đường tròn, chu vi hình tròn, diên tích hình tròn.