Lượng giác là một trong những kiến thức đại số quan trọng trong chương trình toán học lớp 9 vì nó không chỉ thường xuyên xuất hiện trong bài thi tuyển sinh lớp 10 hàng năm mà còn là nền tảng kiến thức cho quá trình học trung học phổ thông sau này. Vì thế hãy cùng Sigma Books hệ thống để nằm lòng các công thức lượng giác lớp 9 và các dạng bài tập liên quan.
Lượng giác là gì?
Lượng giác là một chủ đề toán học thể hiện sự liên hệ giữa các góc và cạnh của một tam giác vuông. Trong đó tỉ số lượng giác của các góc trong tam giác vuông là:
Sin a = cạnh đối / cạnh huyền
Cos a = cạnh kề / cạnh huyền
Tan a = cạnh đối / cạnh kề
Cot a = cạnh kề / cạnh đối
Để nhớ các công thức này, các em học sinh có thể tham khảo mẹ ghi nhớ sau
Sin a = cạnh đối / cạnh huyền —-> Sin đi học
Cos a = cạnh kề / cạnh huyền —-> Cos không hư
Tan a = cạnh đối / cạnh kề —-> Tan đoàn kết
Cot a = cạnh kề / cạnh đối —-> Cot kết đoàn
Vai trò của lượng giác

Lượng giác không chỉ quan trọng đối với toán học mà còn mang tính ứng dụng cao trong nhiều lĩnh vực như thiên văn học, địa lý, âm nhạc…
Nhờ vào các tỉ số lượng giác mà chúng ta ta có thể tính được những khoảng cách không thể tới được như độ dài một khúc sông có hai bờ song song với nhau, chiều cao tòa nhà…
Ngoài ra, tỉ số lượng giác còn có vai trò quan trọng trong lĩnh vực vật lý, đặc biệt là trong nghiên cứu về sóng âm. Âm thanh tạo ra các bước sóng âm có hình dạng như biểu thị của các hàm sin và cos. Vì thế âm thanh có thể được biểu hiện một cách trực quan thông qua hàm lượng giác, tạo tiền đề cho ứng dụng ghi âm kỹ thuật số hiện nay.
GPS hay còn còn lại hệ thống định vị trên mặt đất cũng là một trong những công nghệ ứng dụng hàm lượng giác. GPS hoạt động dựa trên các dữ liệu thu thập từ hệ thống vệ tinh ngoài không gian và các kiến thức về hình học trái đất, sau đó GPS ứng dụng các công thức lượng giác để tính toán và xác định vĩ độ và kinh độ của bạn.
Với những ứng dụng này, chắc hẳn bạn đã hiểu tại sao chúng ta cần nắm chắc các kiến thức về lượng giác cũng như các công thức lượng giác lớp 9 cơ bản mà ta được học.
Các công thức lượng giác lớp 9 cần ghi nhớ

Nếu a và b là hai góc phụ nhau ( a + b = 90°) thì thì sin của góc này sẽ bằng cos của góc kia, đồng thời tan góc này cũng bằng cot góc kia.
Sin a = cos b, cos a = sin b
Tan b = cot b, cot a = tan b
Nếu a và b là hai góc nhọn có hai tỷ số lượng giác sin góc này bằn sin góc kia và cos góc này bằng cos góc kia thì hai góc đó bằng nhau.
Sin a = sin b và cos a = cos b —> a = b
Nếu như a là một góc nhọn bất kỳ với 0 < sin a < 1, 0 < cos a < 1, 0 < tan a < 1, 0 < cot a< 1 thì ta có:
Tan a = sin a / cos α
Cot a = cos a / sin a
Tan a. cot a = 1
Trong bảng lượng giác lớp 9, các tỉ số lượng giác của các góc đặc biệt sau đây cần ghi nhớ
Sin 0° = 0; Cos 0° = 1; tan 0° = 0; cot 0° = kxd
Sin 90° = 1; Cos 90° = 0; tan 90° = kxđ; cot 90° = 0
Sin 30° = 0.5; Sin góc 45° = √2/2; Sin 60° = √3/2
Cos 30° = √3/2 ; Cos 45° = √2/2 ; Cos 60° = ½
Tan 30° = √3/3 ; Tan 45° = 1 ; Tan 60° = √3
Cot 30° = √3 ; Cot 45° = 1 ; Cot 60° = √3/3
Các dạng bài tập trong chuyên đề lượng giác lớp 9
Dạng 1: Xác định tỉ số lượng giác của một góc nhọn
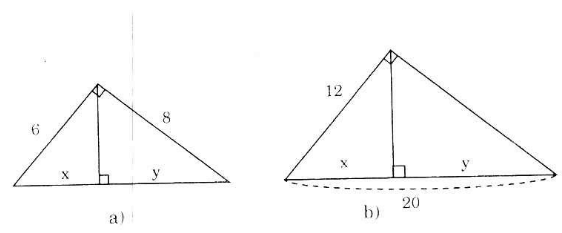
Đây là dạng toán cơ bản trong chuyên đề lượng giác lớp 9. Để làm được dạng toán này, các bạn cần ghi nhớ các công thức lượng giác và áp dụng bảng tỉ số lượng giác lớp 9 để tìm ra đáp án của bài toán.
Ví dụ 1: Cho tam giác vuông ABC như hình vẽ. Trong đó góc B là góc 60 độ và cạnh huyền BC có độ dài là 8. Tìm độ dài của cạnh AC
Lời giải: Ta có B là góc 60 độ nên dựa vào bảng lượng giác:
Sin B = AC/BC
=> AC = Sin B . BC = sin 60°.8 = √3/2.8 = 4√3
Vậy AC = 4√3
Dạng 2: Chứng minh đẳng thức
Đây là dạng toán rất hay xuất hiện trong các đề thi và đề ôn vào lớp 10 môn toán các năm gần đây. Để làm được dạng toán này, các bạn cần ghi nhớ các công thức lượng giác và cách biến đổi linh hoạt giữa các công thức lượng giác với nhau.
Ví dụ 1:
Chứng minh đẳng thức sau:
sin ² a + cos ² a = 1
Lời giải: Dựng tam giác vuông OAB tùy ý, trong đó góc A là góc vuông. Góc đối diện cạnh AB là α
Dựa trên tỉ số lượng giác của góc nhọn, ta có:
sinα = AB / OB và cosα = OA/ OB
Mặt khác tanα = AB/ OA và cotα = OA/ AB.
Ta có
sin α : cos α = (AB/ OB) : (OA/ AB) = AB : OA = tan α
cos α : sin α = (OA/ OB) : ( AB/ OB) = OA/ AB = cot α
tan α x cot α = (AB/ OA) x (OA/ AB) = 1
Áp dụng định lý Pitago trong tam giác vuông OAB có:
OB² = OA² + AB²
Ta có:
Sin ² α + cos ² α = AB²/OB² + OA²/OB²
= (AB² + OA²)/OB² = OB²/OB² = 1
Vậy Sin ² α + cos ² α = 1
Đẳng thức được chứng minh
Một số bài tập tham khảo
Bài 1: Cho tam giác ABC có góc A = 90 độ . Biết cos của gốc B = 0,8, hãy tìm các tỉ số lượng giác của góc C.
Bài 2: Cho tam giác ABC. Cạnh AC và BC vuông góc với nhau. Trong đó cạnh AC có độ dài là 0,9m, BC = 1,2m. Tìm các tỉ số lượng giác sin, cos, tan và cot của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
Bài 3: Chuyển đổi các tỉ số lượng giác sau lần lượt thành tỉ số lượng giác của các góc nhọn nhỏ hơn 45 độ: sin 60° , cos 75° , sin 52°′, cot 82°, tan 80°
Để làm tốt các dạng toán lượng giác, cách duy nhất là các bạn phải ghi nhớ đầy đủ các công thức lượng giác cơ bản và thường xuyên rèn luyện bài tập lượng giác. Hi vọng những chia sẻ trong bài viết này của Sigma Books sẽ phần nào giúp bạn nằm lòng các công thức lượng giác lớp 9 và chinh phục thành công các bài tập liên quan.




