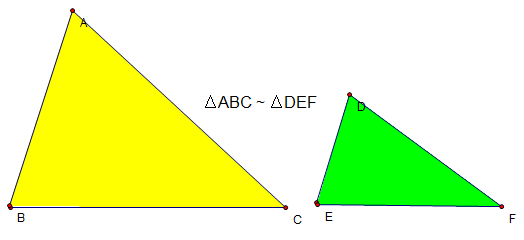
Các trường hợp đồng dạng của tam giác vuông là một trong những bài toán hình học quan trọng nhất trong chương trình lớp 8. Tuy nhiên rất nhiều em học sinh còn chưa thực sự hiểu về bài toán này. Vì thế hãy cùng Sigma Books tìm hiểu các trường hợp đồng dạng của tam giác vuông và thực hành với các dạng toán liên quan bạn nhé.
Như thế nào là hai tam giác vuông đồng dạng?
Hai tam giác vuông đồng dạng với nhau trong trường hợp:
Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia
Ví dụ chứng minh: Cho hai tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’. Trong đó góc A và góc A’. Chứng minh hai tam giác đồng dạng.
Ta có, ∠A = ∠A’ (1)
2 tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’ vì vậy
∠B = ∠B’ = 90º (2)
Trong khi đó ∠C = 180 – (∠A + ∠B) (3)
∠C’ = 180 – (∠A’ + ∠B’) (4)
Từ (1), (2), (3) và (4) dễ dàng suy ra ∠C = ∠C’
2 tam giác vuông ABC và A’B’C’ có: ∠A = ∠A’ ; ∠B = ∠B’ ; ∠C = ∠C’
Suy ra tam giác ABC và A’B’C’ đồng dạng với nhau.
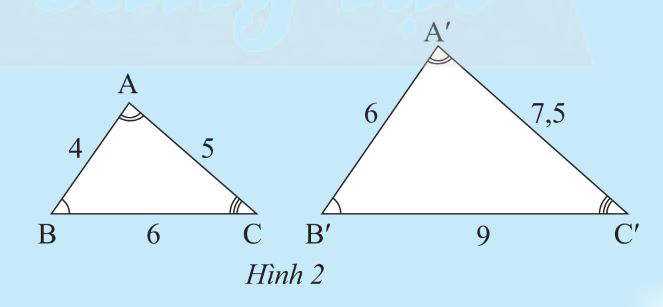
Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
Ví dụ chứng minh: Cho hai tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’. Trong đó góc AB/AB’ = BC/BC’. Chứng minh hai tam giác đồng dạng.
Ta có hai tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’ vì thế:
∠B = ∠B’ = 90º (1)
Theo dữ kiện đề bài ta có: AB/AB’ = BC/BC’ (2)
Từ (1) và (2) dễ dàng chứng minh hai tam giác vuông ABC và A’B’C’ đồng dạng theo trường hợp cạnh – góc – cạnh.
Ví dụ: Cho hai tam giác vuông ABC và A’B’C’ như hình vẽ
Hai tam giác vuông ABC và A’B’C’ đồng dạng với nhau nếu:
Trường hợp 1: Cạnh – cạnh
AB/A’C’ = BC/A’C’ (trong đó AB và AC là hai cạnh góc vuông)
Trường hợp 2: Góc
∠B = ∠B’ hoặc ∠C = ∠C’ (trong đó ∠B và ∠C là hai góc nhọn)
Dấu hiệu nhận biết của hai tam giác vuông đồng dạng
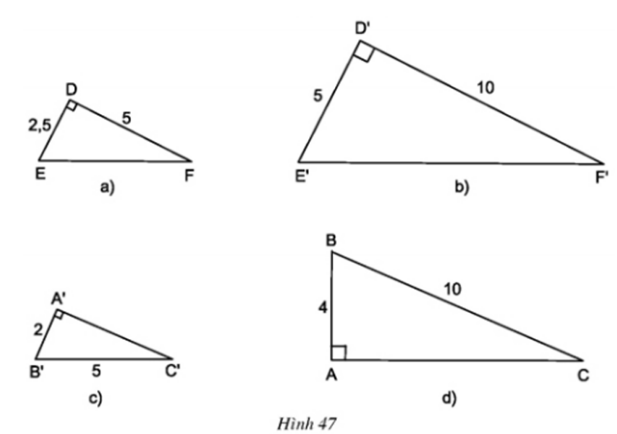
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc
Ví dụ chứng minh: Cho hai tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’. Trong đó góc A’B/AB’ = A’C/AC’
Ta có hai tam giác vuông ABC và A’B’C’ lần lượt vuông góc tại B và B’ vì thế theo định lý Py-ta-go ta có:
AC ² = AB²+ BC² suy ra BC² = AC ² – AB²
A’C’² = A’B’²+ B’C’² suy ra B’C’² = A’C’ ² – A’B’²
Ta có từ dữ kiện đề bài:
AB/A’B’ = AC/A’C’ (1)
⇔ (AB/A’B’)² = (AC/A’C’)²
⇔ AB²/A’B’² = AC²/A’C’²
⇔ AB²/A’B’² = (AB²+ BC²)/(A’B’²+ B’C’²)
⇔ AB².A’B’²+ BC².A’B’² = A’B’²AB²+ B’C’²AB²
⇔ BC².A’B’² = B’C’²AB²
⇔ BC²/B’C’² = AB²/A’B’²
⇔ BC/B’C = AB/A’B (2)
Từ (1) và (2) dễ dàng chứng minh A’B/AB’ = A’C/AC’ = BC/B’C
Vậy hai tam giác vuông ABC và A’B’C’ đồng dạng với nhau.
Tính chất của hai tam giác vuông đồng dạng
Tính chất 1: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng
Tính chất 2: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng
Tính chất 3: Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
Tính chất 4: Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
Tính chất 5: Tỉ số chu vi của hai tam giác bằng tỉ số đồng dạng.
Tính ứng dụng của hai tam giác vuông đồng dạng
Thức tế hai tam giác vuông đồng dạng có tính ứng dụng rất cao trong cuộc sống hàng ngày. Những tính chất về cạnh và góc của hai tam giác vuông đồng dạng là cơ sở giúp các nhà khoa học phát hiện ra cách đo độ cao của một điểm không với tới hoặc đo khoảng cách xa như bên kia bờ sông… Khi đó người ta sẽ dựa trên các tính chất tam giác đồng dạng để tính toán được kích thước chuẩn xác của vật hoặc khoảng cách đó mà không cần phải đo lường trực tiếp. Đây cũng là cơ sở cho rất nhiều công nghệ khoa học kỹ thuật phát triển sau này.
Các dạng bài tập về hai tam giác vuông đồng dạng
Dạng 1: Chứng minh hai tam giác đồng dạng
Với bài toán này, đề bài thường cho hai tam giác cho trước và các dữ kiện liên quan. Nhiệm vụ của các em học sinh là phải chứng minh được hai tam tác đó đồng dạng. Để làm bài toán này, các em cần bán sát theo các định lý và tính chất để nhận biết tam giác đồng dạng.
Ví dụ: Cho tam giác nhọn ABC có BD và CE là hai đường cao cắt nhau tại H. Gọi M là giao điểm của AH và BC. Chứng minh rằng MH.MA = MB.MC.
Tam giác ABC có BD và CE là hai đường cao cắt nhau tại H nên H là trực tâm của tam giác ABC.
Suy ra AB vuông góc với BC
Xét hai tam giác MBH và MAC ( lần lượt vuông góc tại H và M)
Dễ dàng suy ra:
∠MBH = ∠MAC do hai góc cùng phụ với với ∠ACB
Vậy tam giác MBH và MAC đồng dạng với nhau theo trường hợp góc – góc
Theo tính chất của hai tam giác đồng dạng
MB/MA = MH/MC => MH.MA = MC.MB
Dạng 2: Bài toán ứng dụng
Đây là một dạng toán rất hay và sát với thực tế nên ngày càng được xuất hiện nhiều trong các bài kiểm tra và bài thi. Dạng toán này thường cho các dữ liệu cần thiết và yêu cầu đo độ dài hoặc khoảng cách của một vật cho trước. Từ những dữ kiện của bài toán, các em có thể tính toán các số đo cần thiết dựa vào tính chất của 2 tam giác đồng dạng và tìm được đáp án.
Ví dụ: Bóng của cây cổ thụ phủ trên mặt đất có độ dài là 4,5 m.Cùng thời điểm đó,một cây con khác cao 2,1m đứng vuông góc với mặt đất có bóng dài 0,6m.Tính chiều cao của cây cổ thụ.
Kẻ AB và DE lần lượt là cây cổ thụ và cây con
Trong đó AC và DF lần lượt là bóng của hai cây
Biết AC = 4,5 ; DF = 0,6 (m)
Ta có tia sáng mặt trời chiếu song song nên
BC // EF
AB và DE đều vuông góc với mặt đất nên AB // DE
Suy ra góc B = góc E
Hai tam giác ABC và DEF đều là 2 tam giác vuông lần lượt vuông góc tại A và D
Vì thế hai tam giác ABC và DEF đồng dạng nhau.
Khi đó ta có:
AB/DE = AC/DF
AB = AC.DE/DF = 4,5.2,1/0,6 = 15,75 (m)
Vậy cây cổ thụ cao 15,75m
Bài viết trên đây đã tìm hiểu các trường hợp đồng dạng của tam giác vuông cũng như đưa ra các bài toán cụ thể để chứng minh cho từng trường hợp. Đừng quên theo dõi chuyên mục của chúng tôi để cập nhật nhiều thông tin hữu ích mỗi ngày nhé.