Đồng dạng là chuyên đề toán học quan trọng đóng vai trò nền tảng cho kiến thức hình học sau này. Chính vì thế các em học sinh lớp 8 phải ghi nhớ kỹ các tính chất của hai tam giác đồng dạng, dấu hiệu nhận biết và các trường hợp đồng dạng của tam giác vuông… Trong bài viết này, Sigma Books sẽ cùng bạn tổng hợp lại các kiến thức quan trọng này cũng như ôn tập qua những dạng bài tập hay từ cơ bản đến nâng cao về hai tam giác đồng dạng.
Như thế nào là 2 tam giác đồng dạng với nhau?
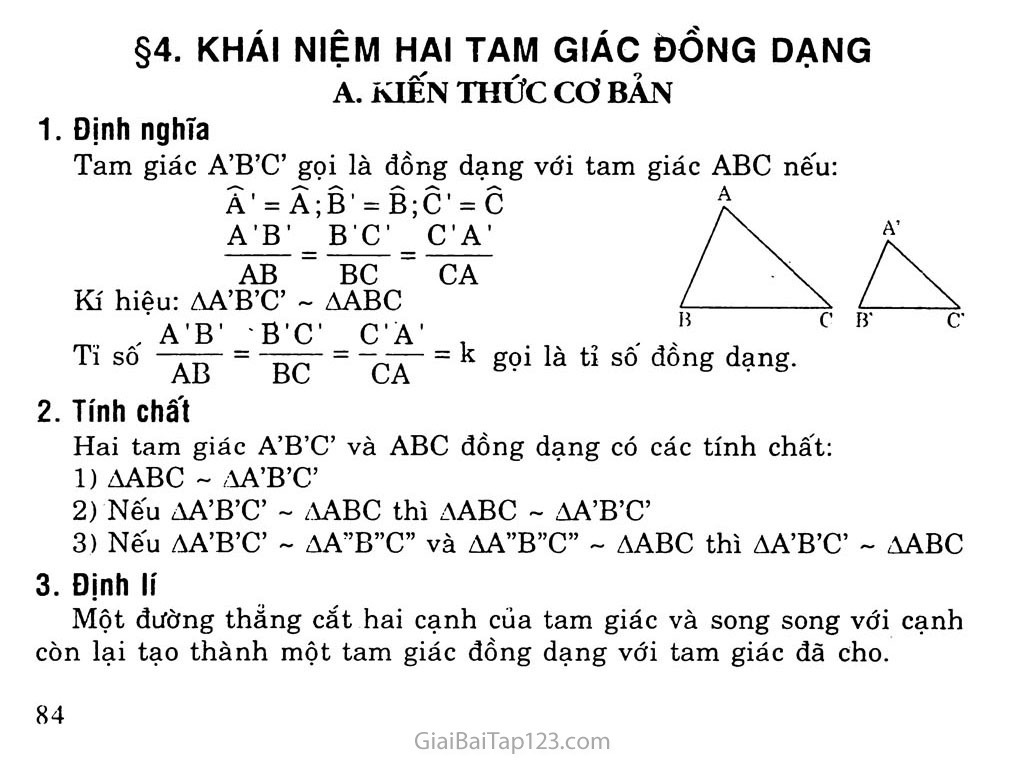
Hai tam giác được định nghĩa là đồng dạng nếu các góc của tam giác này tương ứng bằng các góc của tam giác kia và các cạnh tương ứng tỷ lệ với nhau.
Ký hiệu đồng dạng: ᔕ
Ví dụ: Ta có 2 tam giác ΔABC và ΔEFG. Nếu tam giác Δ ABC đồng dạng với Δ EFG thì ta có:
∠A = ∠E ; ∠B = ∠F ; ∠C = ∠G
AB / EF = BC / FG = AC / EG = k
Tỷ số k giữa các cạnh tương ứng của 2 tam giác đồng dạng
Tổng hợp 3 trường hợp đồng dạng của tam giác
Trường hợp 1: Hai tam giác được xác định là đồng dạng với nhau nếu 3 cạnh của tam giác này lần lượt tỷ lệ với 3 cạnh của tam giác kia.
Ví dụ minh họa: Tam giác ΔABC và tam giác ΔEFG có:
AB/EF = BC/FG = AC/EG thì tam giác ΔABC và tam giác ΔEFG đồng dạng.
Trường hợp 2: Hai tam giác đồng dạng với nhau nếu 2 cạnh của tam này lần lượt tỷ lệ với 2 cạnh của tam giác kia đồng thời góc được tạo bởi hai cặp cạnh đó bằng nhau ở cả 2 tam
giác.
Ví dụ minh họa: Tam giác ΔABC và tam giác ΔEFG có:
AB/EF = BC/FG
Đồng thời ∠B = ∠F
Suy ra tam giác ΔABC và tam giác ΔEFG đồng dạng.
Trường hợp 3: Hai tam giác được xác định là đồng dạng với nhau nếu 2 góc của tam giác này lần lượt bằng 2 góc của tam giác còn lại.
Ví dụ minh họa: Tam giác ΔABC và tam giác ΔEFG có:
∠A = ∠E ; ∠B = ∠F
Suy ra tam giác ΔABC và tam giác ΔEFG đồng dạng với nhau

Khi nào 2 tam giác vuông đồng dạng với nhau ?
Tam giác vuông là tam giác có một góc 90 độ vì thế các trường hợp đồng dạng của tam giác vuông bao gồm:
Trường hợp thứ nhất: Tam giác vuông này có chứa một góc nhọn bằng với góc nhọn của tam giác vuông còn lại.
Ví dụ: Tam giác vuông ABC (∠A = 90 độ) và tam giác vuông IML (∠I = 90 độ) đồng dạng với nhau nếu ∠B = ∠M thì hai tam giác này đồng dạng với nhau
Trường hợp 2: Tam giác vuông này đồng dạng với tam giác vuông kia nếu hai cạnh góc vuông này tỷ lệ với hai cạnh góc vuông kia
Ví dụ: Tam giác ABC vuông tại A và tam giác IML vuông tại I có:
AB/IM = AC/AL
Làm cách nào để nhận biết hai tam giác vuông đồng dạng
Định lý 1: Nếu tam giác vuông này có cạnh huyền và một cạnh góc vuông tỷ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì có thể kết luận hai tam giác đó đồng dạng
Chứng minh định lý.
Cho tam giác ABC và tam giác MNP là 2 tam giác vuông lần lượt vuông tại A và M. Biết BC/NP = AB/MN.
Ta có BC/NP = AB/MN
Suy ra BC²/NP² = AB²/MN²
Ta có
BC²/NP² = AB²/MN² = (BC² – AB²) / (NP²-MN²)
Theo định lý pitago:
BC² – AB² = AC²
NP²-MN² = MP²
Suy ra:
BC²/NP² = AB²/MN² = AC²/MP²
Kết luận tam giác ABC và tam giác MNP đồng dạng với nhau.
- Định lý 2: Nếu 2 tam giác vuông đồng dạng với nhau thì tỉ số giữa 2 đường cao tương ứng của 2 tam giác đó bằng tỷ số đồng dạng.
- Định lý 3: Nếu 2 tam giác vuông đồng dạng thì tỷ số giữa diện tích của tam giác này bằng tỷ số đồng dạng.
Trên đây là các trường hợp đồng dạng của tam giác vuông và một số bài tập liên quan. Hi vọng rằng sau bài viết này, các em sẽ nắm được những kiến thức cơ bản về tam giác đồng dạng cũng như ứng dụng thành thạo bài toán đồng dạng trong cuộc sống.




